原函数与不定积分的概念：

原函数的定义：在区间【a，b】上，若F(x)=f(x)

则称F((x)是在【a，b】上原函数

函数f(x)在[a,b]上连续，f(x)在[a,b]上可积

函数f(x)在【a,b]上有界，且只有有限个间断点，f(x)在[a,b]可积

曲线的渐近线：若曲线C上的点M沿着曲线无限地远离原点时，点M与某一直线L的距离趋于0，则称直线L为曲线C的渐近线

函数单调性的判定法：

定理1：设函数f(x)在开区间I内可到，若f'(x)>0,（f'(x)<0),则f(x)在I内单调递增（递减）

中值定理：

应用：研究函数性质及曲线性态；利用导数解决实际问题

费马引理：y = f(x)在U(x0)有定义，且f(x)<=f(x0),f'(x0)存在，即f'(x0）= 0

罗尔定理：

y = f(x)满足：

1.在区间[a,b]上连续

2.在区间[a,b]内可导

3.f(a)=f(b),，在（a,b)内至少存在一点

拉格朗日中值定理：

一、什么是高等数学？

初等数学--研究对象为常量，以精致观点研究问题。

高等数学--研究对象为变量，运动和辩证法进入了数学。

数学中的转折点是笛卡尔的变数。有了变数，运动进入了数学，有了变数，辩证法进入了数学，有了变数，微分和积分也就立刻成为必要的了，而它们也就立刻产生。--恩格斯

主要内容：

1、分析基础：函数，极限，连续

2、微积分学：一元微积分（上册）、多元微积分（下册）

3、向量代数与空间解析几何

4、无穷级数

5、常微分方程

二、如何学习高等数学？

1、认识高等数学的重要性，培养浓厚的学习兴趣。

一门科学，只有当他成功地运用数学时，才能达到真正完善的地步。--马克思

要辩证而又唯物地了解自然，就必须熟悉数学。--恩格斯

2、学数学最好的方式是做数学。

聪明在于学习，天才在于积累。学而优则用，学而优则创。由薄到厚，由厚到薄。--华罗庚

第一章 函数与极限

分析基础：函数--研究对象

                 极限--研究方法

                 连续--研究桥梁

第一节 映射与函数

一、集合

1、定义及表示法

定义1、具有某种特定性质的事物的总体称为集合。组成集合的事物称为元素。

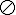空集，

元素a属于/不属于集合M,记作,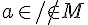

注：M为数集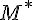：排除0的数集

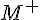                       排除0和负数的数集

表示法：（1）列举法 （2）描述法

2、集合之间的关系及运算

定义2 包含关系：A是B的子集，B包含A

空集是任意集合的子集

B包含A，C包含B，则C包含A

A包含B，B包含A，则A=B

定义3 运算：并集、交集、差集、余集、直积

二、映射

三、函数

隐函数的导数：若由方程F(x,y)=0可去欸的那个y是x的函数，则称此函数为隐函数

由y=f(x)表示的函数，称为显函数

高阶导数：

导数的几何意义：

曲线y= f（x）在点（X0，Y0）的切线斜率为tana = f'(X0)

若f'(X0)>0，曲线过（X0，Y0)上升；

若f'(X0)<0，曲线过（X0,Y0)下降；

若f'(X0)=0,切线与X轴平行，X0称为驻点

若f'(X0)=无穷大，切线与X轴垂直；

f'(X0)不等于无穷大时，曲线在点（X0,Y0)处的切线方程：y-y0 = f'(x0)(x-x0)

导数与微分：

导数：描述函数变化快慢

微分：描述函数变化程度

曲线的切线斜率：y = f(x)在M点处的切线

斜率：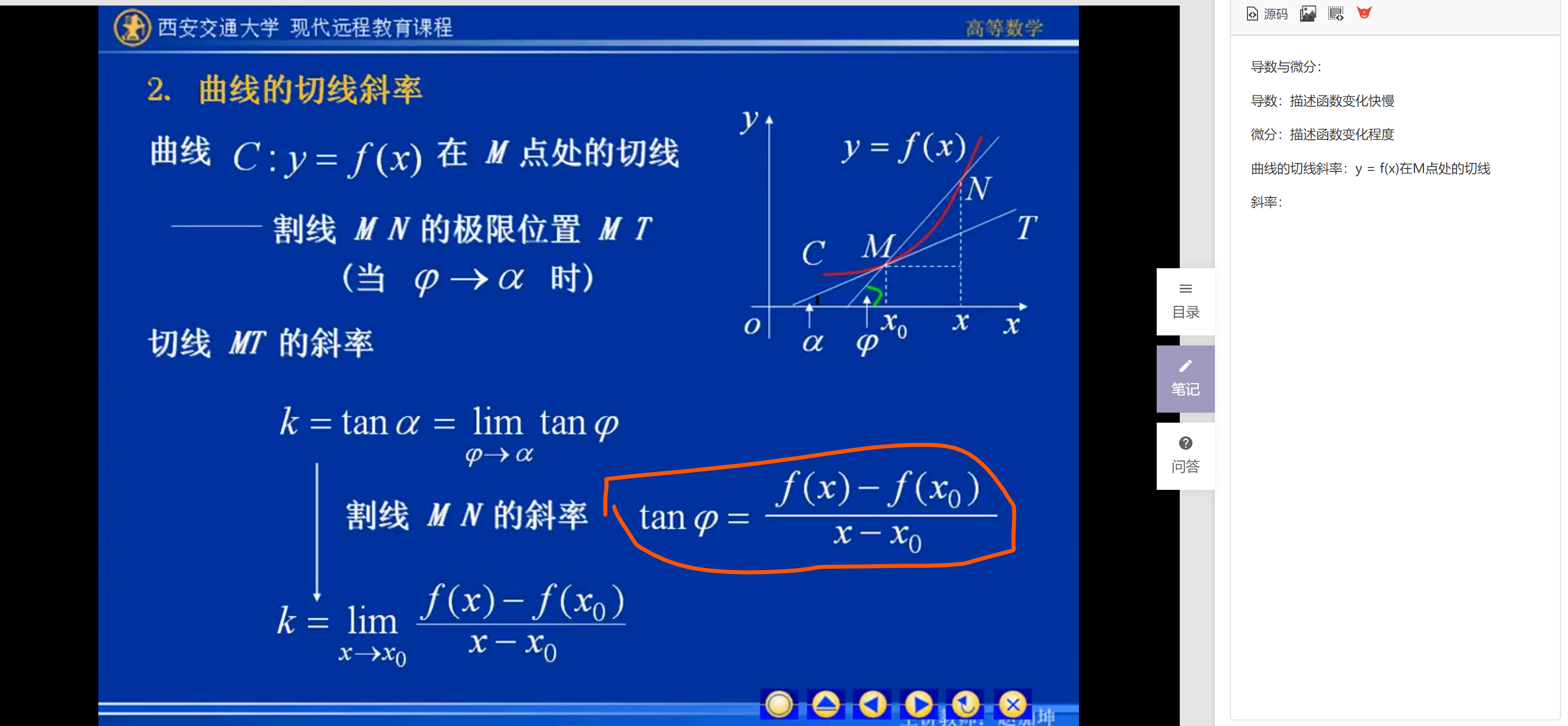

最值定理：在闭区间上连续的函数，在该区间上一定有最大值和最小值

一切初等函数在定义区间内连续

若f(x)在某区间上没一点都连续，则称它在该区间上连续，或称它为该区间上的连续函数，在区间[a,b]上的连续函数的集合记作：C[a,b]

定义：设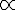，白塔是自变量 同一变化过程中的无穷小，若lim白塔除以阿尔法=0，则白塔是比阿尔法高阶的无穷小，记作白塔=o(阿尔法）

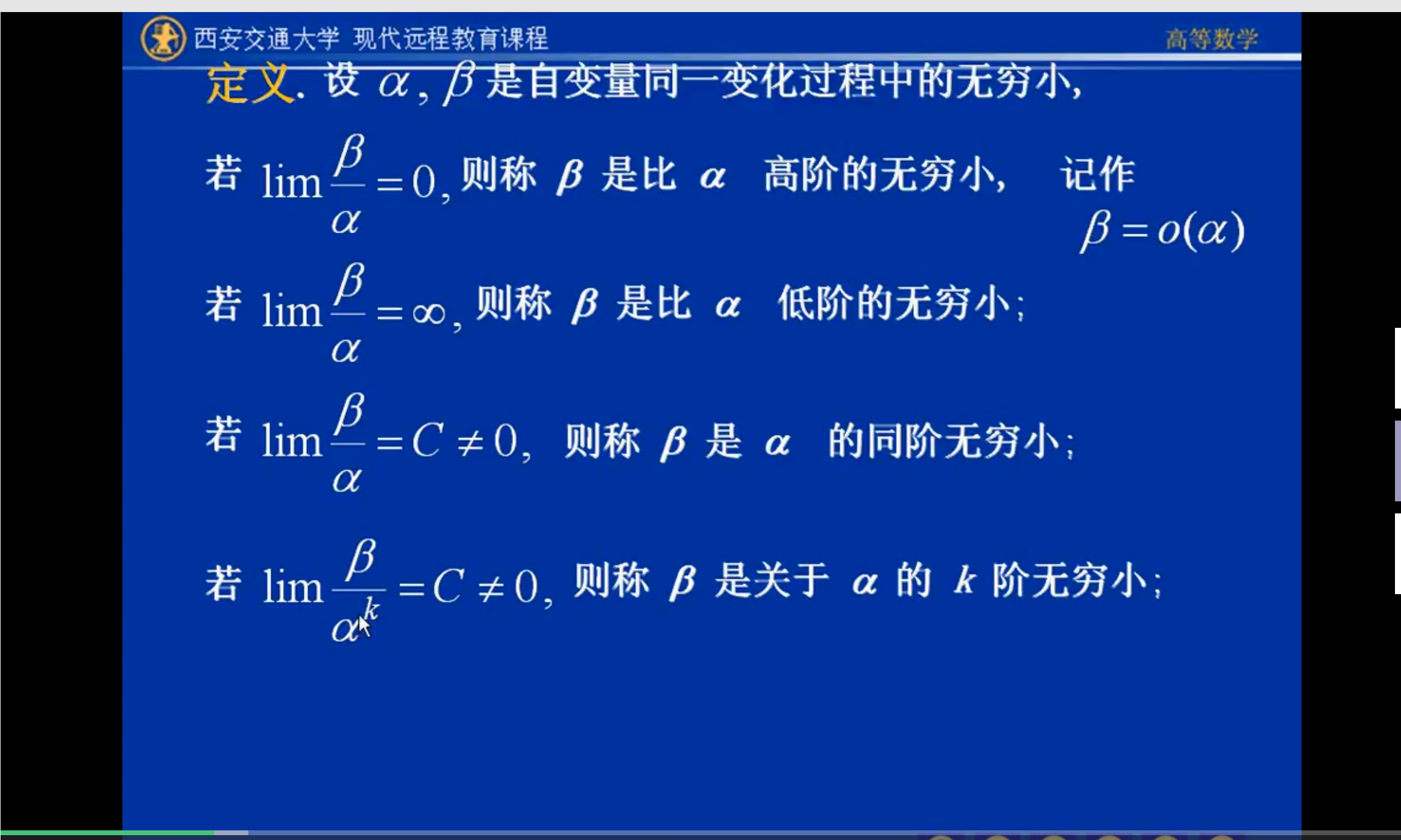
有限个无穷小的和还是无穷小

无限个无穷小之和不一定是无穷小

有界函数与无穷小的乘积是无穷小

常数与无穷小的乘积是无穷小

1.若x->x0时，函数f(x)->0,则函数f(x)为x->x0是的无穷小

说明：除0意外任何很小的常数都不是无穷小

2.无穷大：若任给M>0,总存在德尔塔>0,使对一切满足不等式0<|x-x0|<德尔塔的x,总有|f(x)|>M,则称函数f(x)当x-x0时为无穷大

3.无穷下与无穷大的关系：

在自变量的同一变化过程中，若f(x)为无穷大，则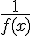为无穷小，若f(x)为无穷小，且f(x)不等于0，则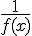为无穷大